В-8 (РГР-ТВ-itr)

Купить решение

1.8. Сколько различных четырехзначных чисел можно записать с помощью девяти значащих цифр, из которых ни одна не повторяется?

2.8. На полке 6 радиоламп, из которых две негодные. Случайным образом отбираются две радиолампы. Какова вероятность того, что они годны для использования?

3.8. Трое рабочих собирают подшипники. Вероятность того, что подшипник, собранный первым рабочим, — высшего качества, равна 0,7, вторым – 0,8, третьим – 0,6. Для контроля взято по одному подшипнику из собранных каждым рабочим. Какова вероятность того, что высшего качества будут:

а) все подшипники;

б) два подшипника;

в) хотя бы один подшипник?

4.8. В дисплейном классе имеется 10 персональных компьютеров первого типа и 15 второго типа. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,9, а на компьютере второго типа – 0,7. Найти вероятность того, что:

а) на случайно выбранном компьютере за время работы не произойдет сбоя;

б) компьютер, во время работы на котором не произошло сбоя, — первого типа.

5.8. При массовом производстве полупроводниковых диодов вероятность брака при формовке равна 0,1. Найти вероятность того, что из восьми диодов, проверяемых ОТК, бракованных будет:

а) два;

б) не менее двух;

в) не более двух.

6.8. Среднее число машин, прибывающих в автопарк за 1 мин, равно двум. Найти вероятность того, что за 5 мин прибудет не менее двух машин, если поток прибытия машин простейший.

7.8. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(Х) и среднее квадратическое отклонение G(X). Построить график функции распределения F(x). Вероятность попадания вызова на АТС в течение 1 мин равна 0,4; СВ Х – число вызовов, поступивших на АТС за 4 мин.

8.8. Дана функция распределения F(x) СВ Х. Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания СВ Х на отрезок [a,b]. Построить графики функций F(x) и f(x).

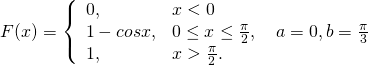
9.8. Считается, что изделие – высшего качества, если отклонение его размеров от номинальных не превосходит по абсолютной величине 3,6 мм. Случайные отклонения размера изделия от номинального подчиняются нормальному закону со средним квадратичным отклонением, равным 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего качества среди 100 изготовленных.

10.8. Вероятность того, что наугад выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,1. Партия изделий не принимается при обнаружении не менее 10 бракованных изделий. Сколько надо проверить деталей, чтобы с вероятностью 0,6 можно было утверждать, что партия, имеющая 10% брака, не будет принята?

Купить решение