Купить решение
1.2. Пять пассажиров садятся в электропоезд, состоящий из 10 вагонов. Каждый пассажир с одинаковой вероятностью может сесть в любой из 10 вагонов. Определить число всех возможных вариантов размещения пассажиров в поезде.
2.2. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлеченный кубик будет иметь две окрашенные грани.
3.2. На железобетонном заводе изготавливают панели, 90 % из которых – высшего сорта. Какова вероятность того, что из трех наугад выбранных панелей высшего сорта будут:
а) три панели;
б) хотя бы одна панель;
в) не более одной панели?
4.2. Детали попадают на обработку на один из трех станков с вероятностями, равными соответственно 0,2; 0,3; 0,5. Вероятность брака на первом станке равна 0,02, на втором – 0,03, на третьем – 0,01. Найти:
а) вероятность того, что случайно взятая после обработки деталь – стандартная;
б) вероятность обработки наугад взятой детали на втором станке, если она оказалась стандартной.
5.2. В семье четверо детей. Принимая равновероятным рождение мальчика и девочки, найти вероятность того, что мальчиков в семье:
а) три;
б) не менее трех;
в) два.
6.2. Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что в 144 испытаниях событие наступит 120 раз.
7.2. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(Х) и среднее квадратическое отклонение G(X). Построить график функции распределения F(x). Производятся три выстрела по мишени. Вероятность поражения мишени первым выстрелом равна 0,4, вторым – 0,5, третьим – 0,6; СВ Х – число поражений мишени.
8.2. Дана функция распределения F(x) СВ Х. Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания СВ Х на отрезок [a,b]. Построить графики функций F(x) и f(x).
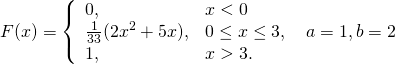
9.2. При определении расстояния радиолокатором случайные ошибки распределяются по нормальному закону. Какова вероятность того, что ошибка при определении расстояния не превысит 20 м, если известно, что систематических ошибок радиолокатор не допускает, а дисперсия ошибок равна 1370 м кв. ?
10.2. Дисперсия каждой из 4500 независимых, одинаково распределенных случайных величин равна 5. Найти вероятность того, что среднее арифметическое этих случайных величин отклонится от своего математического ожидания не более чем на 0,04.



















![]:-> ]:->](https://reshiuniver.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)

























