В-29 (РГР-ТВ-itr)

Купить решение

1.29. На диске телефонного аппарата имеется 10 цифр. Каждый телефон АТС имеет номер, записываемый с помощью пяти цифр, причем первая цифра у них одна и та же. Найти наибольшее возможное число таких абонентов этой станции, у которых 4 последние цифры номера телефона различны.

2.29. В партии, состоящей из 20 радиоприемников, 5 неисправных. Наугад берут 3 радиоприемника. Какова вероятность того, что в число выбранных войдут 1 неисправный и 2 исправных радиоприемника?

3.29. Инженер выполняет расчет, пользуясь тремя справочниками. Вероятности того, что интересующие его данные находятся в первом, втором, третьем справочниках, равны соответственно 0,6; 0,7; 0,8. Найти вероятность того, что интересующие инженера данные содержатся:
а) только в одном справочнике;
б) только в двух справочниках;
в) во всех трех справочниках.

4.29. На сборку поступают детали с четырех автоматов. Первый обрабатывает 40%, второй – 30%, третий – 20% и четвертый – 10% всех деталей, поступивших на сборку. Первый автомат дает 0,1% брака, второй – 0,2%, третий – 0,25%, четвертый – 0,5%. Найти вероятность того, что:
а) на сборку поступит стандартная деталь;
б) поступившая на сборку стандартная деталь изготовлена первым автоматом.

5.29. Среди деталей, изготавливаемых рабочим, в среднем 4% бракованных. Найти вероятность того, что среди взятых на контроль пяти деталей:
а) две бракованные;
б) хотя бы одна бракованная;
в) не более одной бракованной.

6.29. Средняя плотность болезнетворных бактерий в 1 м кб. воздуха равна 100. Берется на пробу 2 дм кб. воздуха. Найти вероятность того, что в нем будет обнаружена хотя бы одна бактерия.

7.29. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(Х) и среднее квадратическое отклонение σ(Х). Построить график функции распределения F(x). Из 39 приборов, испытываемых на надежность, 5 высшей категории. Наугад взяли 4 прибора; СВ Х – число приборов высшей категории среди отобранных.

8.29. Дана функция распределения F(x) СВ Х. Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания СВ Х на отрезок [a;b]. Построить графики функций F(x) и f(x).

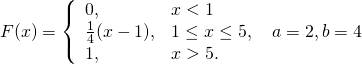
9.29. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение СВ Х, распределенной равномерно в интервале (8; 14).

10.29. Среднее квадратичное отклонение ошибки измерения азимута равно 0,5 градуса, а ее математическое ожидание – нулю. Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 1 градуса.

Купить решение