В-15 (РГР-ТВ-itr)

Купить решение

1.15. Сколькими различными способами можно избрать из 15 человек делегацию в составе трех человек?

2.15. Буквенный замок содержит на общей оси 5 дисков, каждый из которых разделен на 6 секторов с различными нанесенными на них буквами. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Определить вероятность открытия замка, если установка произвольная комбинация букв.

3.15. Два бомбардировщика преодолевают зону ПВО. Вероятность того, что будет сбит первый бомбардировщик, равна 0,7, второй – 0,8. Найти вероятность:

а) уничтожения одного бомбардировщика;

б) поражения двух бомбардировщиков;

в) промахов.

4.15. На сборку поступают детали с трех конвейеров. Первый дает 25 %, второй – 30 % и третий – 45 % деталей, поступающих на сборку. С первого конвейера в среднем поступает 2 % брака, со второго – 3 %, с третьего – 1 %. Найти вероятность того, что:

а) на сборку поступила бракованная деталь;

б) поступившая на сборку бракованная деталь – со второго конвейера.

5.15. Оптовая база обслуживает 6 магазинов. Вероятность получения заявки базой на данный день для каждого из магазинов равна 0,6. Найти вероятность того, что в этот день будет:

а) пять заявок;

б) не менее пяти заявок;

в) не более пяти заявок.

6.15. Станок состоит из 2000 независимо работающих узлов. Вероятность отказа одного узла в течение года равна 0,0005. Найти вероятность отказа в течение года двух узлов.

7.15. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(Х) и среднее квадратическое отклонение G(X). Построить график функции распределения F(x). Двое рабочих, выпускающих однотипную продукцию, допускают производство изделий второго сорта с вероятностями, соответственно равными 0,4 и 0,3. У каждого рабочего взято по 2 изделия; СВ Х – число изделий второго сорта среди них.

8.15. Дана функция распределения F(x) СВ Х. Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания СВ Х на отрезок [a,b]. Построить графики функций F(x) и f(x).

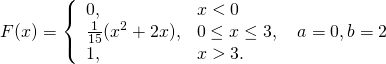
9.15. Из пункта С ведется стрельба из орудия вдоль прямой СК. Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратичным отклонением 5 м. Определить (в %), сколько снарядов упадет с перелетом от 5 до 70 м.

10.15.Вероятность появления события в отдельном испытании равна 0,6. Применив теорему Бернулли, определить число независимых испытаний, начиная с которого вероятность отклонения частоты события от ее вероятности, по абсолютной величине меньшего 0,1, больше 0,97.

Купить решение