В-18 (РГР-ТВ-itr)

1.18. Сколько различных пятизначных чисел можно записать с помощью цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 (без повторений)?

2.18. На полке случайным образом расставляются 10 книг. Определить вероятность того, что при этом три определенные книги окажутся стоящими рядом.

3.18. При некоторых определенных условиях вероятность сбить самолет противника из первого зенитного орудия равна 0,4, из второго – 0,5. Сделано по одному выстрелу. Найти вероятность того, что:

а) самолет уничтожен двумя снарядами;

б) самолет поражен хотя бы одним снарядом;

в) ни один снаряд не попал в цель.

4.18. У сборщика 16 деталей, изготовленных на заводе № 1, и 10 деталей, изготовленных на заводе № 2. Вероятности того, что детали выдержат гарантийный срок, равны соответственно для деталей с завода № 1 – 0,8; с завода № 2 – 0,9.

а) Найти вероятность того, что взятая наугад деталь проработает гарантийный срок.

б) Взятая наугад деталь проработала гарантийный срок. На каком из заводов она вероятнее всего изготовлена?

5.18. Продукция, поступающая из цеха в ОТК, не удовлетворяет условиям стандарта в среднем в 8% случаев. Найти вероятность того, что из наугад взятых семи изделий не удовлетворяют условиям стандарта:

а) шесть изделий;

б) не менее шести изделий;

в) менее шести изделий.

6.18. Вероятность появления события в каждом из 2000 независимых испытаний равна 0,7. Найти вероятность того, что событие наступит не менее 1500 раз.

7.18. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(Х). Вычислить математическое ожидание M(x), дисперсию D(Х) и среднее квадратическое отклонение G(X). Построить график функции распределения F(X). В первой коробке 10 сальников, из них 2 бракованных, во второй – 16 сальников, из них 4 бракованных, в третьей – 12, из них 3 бракованных; СВ Х – число бракованных сальников при условии, что из каждой коробки взято наугад по одному сальнику.

8.18. Дана функция распределения F(x) СВ Х. Найти плотность распределения вероятностей f(x), с математическое ожидание M(X), дисперсию D(X) и вероятность попадания СВ Х на отрезок [a,b]. Построить графики функций F(x) и f(x).

$\begin{displaymath} F(x) = \left\{ \begin{array}{ll} 0, & x< 0\\ \frac{x^3+3x}{14}, & 0 \le x \le 2, \quad a=0, b=1\\ 1, & x>2. \end{array} \right. \end{displaymath}$

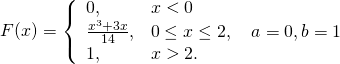
9.18. Минутная стрелка часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с.

10.18. В результате 200 независимых опытов найдены значения СВ

$X_1, X_2,..., X_{200}$